勝手読み

勝手読み

３．１４

「３．１４」という数字を見たり、「サンテンイチヨン」という音を聞いたとき、あなたは何を最初に思い浮かべますか？いまこれを読んでいるほとんどの人は、おそらく「円周率」を連想したのではないでしょうか。でも、あと何年かすると「なにそれ？」なんて言われてしまうかもしれませんねぇ。なんでも、新しい教科書では円周率を「３」と教えるそうですから。　そもそも円周率は記号　π　で表される無理数なんで、「３．１４」であろうが「３」であろうが、どっちにしても近似値なんだから、計算に楽な「３」を使ったって本質的な違いは無い、という理屈は分からなくもないです。しかし、そこまで単純化してしまって良いものでしょうかねぇ。誤差５％弱が多いか少ないか、それは時と場合に依るでしょうが、なんだかチョット心配です。例えば、画用紙を使って直径１０センチの円柱を作ってみることになったとします。底とテッペンの円盤はコンパスを使って簡単に作れます。のりしろを１センチ取ったにしても、直径１２センチの円の内側に直径１０センチの円を書いてハサミで切り取るだけです。でも、側面に使う長方形を画用紙から切り出すとき必要な、辺の長さを計算する際に円周率を「３」で計算したらとんでもないことになってしまいます。せっかく誤差調整用「のりしろ１センチ」を取ったとしても、残念ながらなんの役にも立ちません。しかしまぁ、逆説的に言えば、この工作によって「円周率は３ではない」ことに気が付くきっかけになるのは良いことかもしれません。「３．１４」で教えた場合は「円周率は３．１４ではない」ことに気が付く可能性はほとんどありませんから。　物事を単純化して考える手法はいろんな場面でよく使われます。単純化によって見えにくいものが見えてくるのがその理由でしょうが、反面、単純化によって大事なものまで一緒に失われてしまう可能性もあることを心得ておくべきでしょう。そして、単純化の目的に応じた丁度良い線というものもあるのではないでしょうか。（最近はネタが薄いんで前振りが長い。すみません。）　さて、碁でも単純化の手法をよく使います。９路盤などは良い例で、いきなり１９路盤で始めるのに比べると格段に取っ付きやすくなっています。しかし、それでもまだ結構複雑で、例えばルールなどについて考察するのには十分単純化されているとはいえません。このサイトでも５路盤とか７路盤とか使っていますが、今回はもっと小さい盤を考えます。円周率に因んで３路盤に挑戦してみましょう。
図１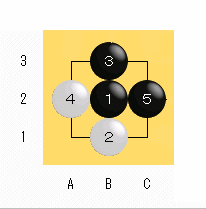	３路盤だと左図の手順が面白いです。これでもう白は打つ手がありません。（と、私は思います。）　白６、パス。　黒７、パス。白が全滅で、黒８目勝ち。さて、この結論は正しいのでしょうか。
図２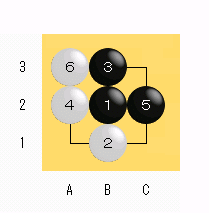	もし、白が６をパスせず左図の様に打ったとしたら？黒はやっぱりパスでしょう。　黒７、パス。　白８、パス。（これは仕方ないでしょう）私はやはり白全滅で、黒９目勝ち（上図と比べると白１目損）だと思うのですが、白石３子が死である事の証明を要求されたらちょっと悩ましいかもしれません。Ｃ１からは詰められませんから、４と６の白を取る他ありませんが・・・。
図３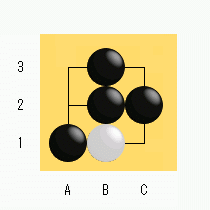	この形は白がＡ２に打ってＡ１の黒を取り返せる姿です。しかし、白が取り返すと図１と同型になります。日本囲碁規約ではコウ以外の同型反復を禁止しておらず、対局者が同意すれば「無勝負」で、合意できなれば「両負け」です。と、私は解釈しています。でも、この解釈、ホントに正しいのでしょうか。なんだか不自然です。きっとどこか解釈を誤っていると思うのですが、良く分かりません。
図４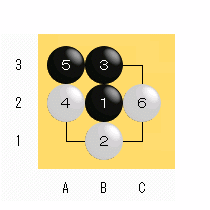	もし、以上の様な混乱を黒が避けるとすると、左図の手順が考えられます。
図５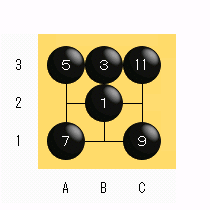	白はコウ立てがありませんから、白８、１０をパスする他ありません。　ハマは３個で、黒６目勝ちとなりました。　図１の解釈よりも黒２目損です。　黒としては図１の解釈で決着したいのですが、図２の問題がある。　悩ましいです。
いかがですか？　３路盤も面白いでしょ？もしこれを中国ルールでスコア計算すると、図１でも図５でも、どちらも同じく黒４．５子勝ちとなります。なんの悩みもありません。こんな事を言うと、わたしが中国ルール贔屓のように思われるかもしれませんが、それは誤解です。次回は、もう一つの極限を使って「日本ルールのここが素敵」について考えます。なお、「日本囲碁規約」を読みたい人には「日本棋院のホームページから日本囲碁規約」を参照してください。　ところで、「３」から何を連想しますか？　私の世代だと最初に浮かぶのは「長島」かなぁ。次の世代は「３」から何を連想するだろうか。「円周率」でない事は確かでしょうねぇ。「円周率を連想する言葉が一つ失われるかもしれない。」そのことが、新しい教科書の持つ大きな問題の一つの様な気がします。

勝手読みメニュー